课程笔记：矩阵理论(34)——盖尔圆定理与特征值估计

Note: 中间欠缺了很多部分，有空慢慢填坑。

矩阵的盖尔圆盘

阶矩阵，每一行可以定义一个盖尔圆盘，每一列也可以定义一个盖尔圆盘。这里先讨论行的情况(关于行的盖尔圆盘)。 圆的半径是除对角元素外所有元素的模的和。圆心是对角线元素(由于是复数，在复平面上有实轴和虚轴坐标)。

这些圆盘区域的并能够得到盖尔区域。

盖尔圆盘定理

盖尔圆盘定理: 设 是n阶矩阵，矩阵的所有特征值一定会落在某个圆盘里。

Proof: 从第四行，挑选特征向量最大的分量 ，并把该分量index 作为选取的矩阵的行。也就是说特征值满足的不等式，是在特征向量中分量最大的位置对应的行。

例3.4.4

注意：有的圆盘可能有多个特征值，有的圆盘可能没有特征值。如果需要精细的描述，使用精细圆盘定理，一个联通区域有几块圆盘，那么该区域必须恰好有相同个数的特征值

例3.4.5

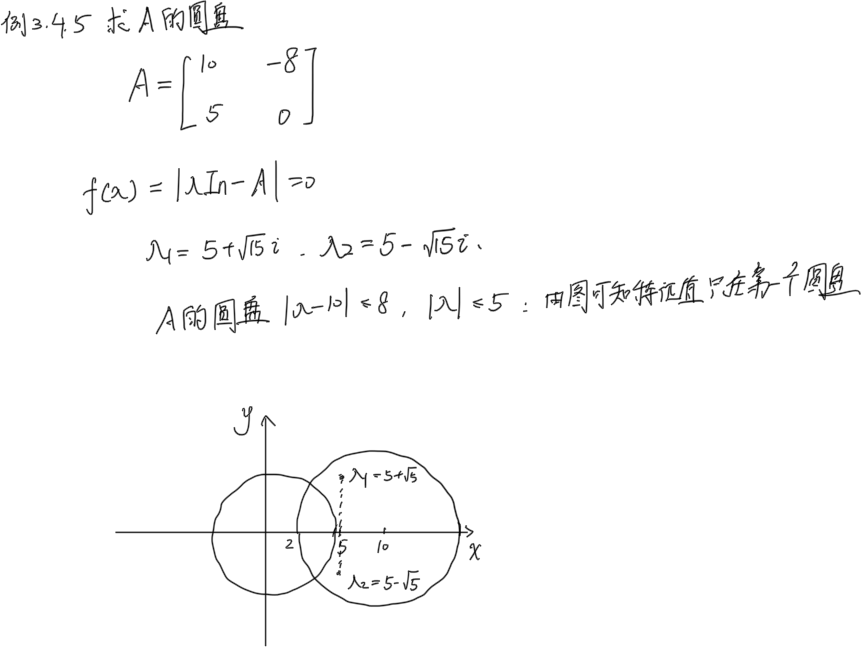
Note : 圆盘定理不能保证每个圆盘一定有特征值。但是下面精细圆盘定理更详细的说明了特征值分布特点：K个圆盘的并集联通区域一定恰好有K个特征值。

精细圆盘定理

精细圆盘定理：设 是盖尔区域的一个由个圆盘组成的连通分量，则恰好有个特征值。

证明思路: 设矩阵, 其中 是对角阵， 是对角线为0的剩余部分。 ,这样矩阵 从对角阵连续变化到原矩阵。对角阵的圆盘半径为0，圆心就是特征值，因此每个圆盘恰好有1个特征值，圆盘外面有 个特征值。在 连续变化增长到1的过程中，圆盘半径逐渐变大，并且部分圆开始相交， 个圆盘相交， 个圆盘区域外有 个特征值。由于矩阵的特征多项式的根是其系数的连续函数，随意特征值也是从圆心出发连续游走的，不会出现跳跃的情况，且增长过程中一直被圆盘包着，所以保证了联通的k个盖尔圆一定恰好有 个特征值。

调节圆盘大小的技巧

如何调整矩阵盖尔圆的半径，从而将特征值分离出来(比喻：就好像化学试剂提纯，分离似的)

原理如下：

首先看出对角线元素是不受影响的，非对角先元素会被放缩，放缩系数由该元素的行与列(对应的是其他行)的系数决定

某一行的放缩系数 和其余行系数 的关系如下：

若 ，为了简便起见，我们设除了第 行的其他行均为1。第 行的非对角元素放缩系数分母比分子大，故圆盘被缩小；其他行的第 列元素分子比分母大，会被放大，除第 列外的其他非对角元素不变，总体圆盘会被放大。

若 ，类似的，设置除了第 行的其他行均为1。只有第 行的圆盘会被放大，其余圆盘均缩小。

利用圆盘定理估计谱半径

矩阵的谱半径 , 并记录

证明思路: 因为根据圆盘定理，矩阵的每个特征值都一定落在某个圆盘(比如)里。 同理，矩阵的谱半径小于某个“最大”的列

其他估计

1. Ostrwoski 圆盘定理

2. Brauer定理(Cassini卵形)