课程笔记：矩阵理论(1)——线性代数知识回顾(上)

📚书籍：《矩阵理论与应用》张跃辉 Chap 1

梦开始的地方：

约定本课程讨论均在复数域的子域上进行。

引言： 线性代数是什么

本科阶段的线性代数课程讨论两个相关问题：一个是引入矩阵来解线性方程组，另一个是利用线性方程组来研究矩阵。

矩阵解线性方程组

可以通过研究齐次方程组

的解结构来来研究的解结构，任意解可以表达为基础解系的线性组合。

展开可详细回顾线性方程组求解

截图自《线性代数》第二版 居余马著 P47 - P48

矩阵提供二次型的简洁表达

请熟悉这个形式和上面的推导过程~系数矩阵 中的每一项 对应的 与的乘积的系数。假如是一个对角矩阵的话，那么就是标准型，（就好比二维平面上的圆），有交叉项的话好比二维平面的椭圆。一定是一个对称矩阵，因为的系数就是的系数。

矩阵乘法与二次型的关系

如何理解阶方阵的高次幂?

相似矩阵, 。如果利用特征值与特征向量可将，那么, 。

此外实对称矩阵可以正交对角化，即存在正交矩阵，使得

可以利用坐标变换 将实二次型化为标准型

矩阵的基础运算及其性质

共轭转置

1. 的共轭矩阵记作，的共轭转置矩阵记作, 当,时，
2. 的矩阵被称为Hermite矩阵，其中当是实对称矩阵。

矩阵乘法

矩阵乘法可以按照行向量进行, 比如对于与的两个矩阵相乘 前一个矩阵的每一行乘以后一个矩阵的每一列，得到新矩阵的每一个元素。

其中，当 是一个(列向量)时,

这里，可以把第一个矩阵摆成行组成的列向量形式，也可以摆成列的行向量的形式。其中第一种形式比较容易理解，因为这就是高斯消元法中个线性方程组联立在一起的形式。但是第二种形式特别容易出错，搞晕，因为第二种形式的线性组合是数乘向量求和的形式，多做几遍就熟悉了。

第二种形式的意义：矩阵乘一个列向量相当于矩阵所有列的线性组合。

同样的，一个行向量乘矩阵相当于矩阵所有行的线性组合，即

因此矩阵乘法,可以看做的每一列，都是每一列的线性组合，组合系数是的对应列；的每一行可以看做是 的每一行的线性组合，组合系数是的对应行。若，那么的每一列向量都是的齐次方程组的解。同理，的每一行也是的齐次方程组的解。

方阵的多项式

称为的多项式。易知，，同一方阵的多项式是可以交换的。

行列式，迹，伴随矩阵，逆，秩等性质

行列式

3. 当时， 必有,必有(满秩矩阵齐次方程有唯一解，就是0解)。
4. 求解二阶行列式对角线法，求解三阶行列式用沙路法。求解阶行列式用递推法（如下按照第行展开） (代数余子式忘了的自己wiki去)。最后完全展开的结果有项，每一项都是不同行不同列元素乘积，然后一半是正号，一半是负号。
5. n阶方程组有克莱默法则，理论意义上解释了线性方程组和其系数的关系。

矩阵的迹

2. （如果分别是和的矩阵即可）

3. （所有元素的平方和，故）

矩阵的秩

1. 定义：矩阵所有不为0的子式中最高的阶数为矩阵的秩
2. 如果一个矩阵的秩为1，那么一定存在列向量, 使得(列向量x行向量，得到矩阵的每一行都是，显然任意两行都线性相关)。那么计算矩阵高次幂时
3. 矩阵和和乘积的秩有如下不等式()：

想看证明请展开

截图自^[1]P6

伴随矩阵，逆矩阵

1. 伴随矩阵(如果是实矩阵通常用，否则常用表示，个人喜好，即便是在复数域上也喜欢用表示，敬请理解)。(证明可参考^[1]中2.2节例题6)

5. 可逆矩阵与任何矩阵乘积不会改变原矩阵的秩

6. 矩阵满秩，非奇异，可逆三者概念等价

分块矩阵

分块矩阵是一种非常好用的技巧。

1. 分块矩阵的加法和数乘就不说了🐒

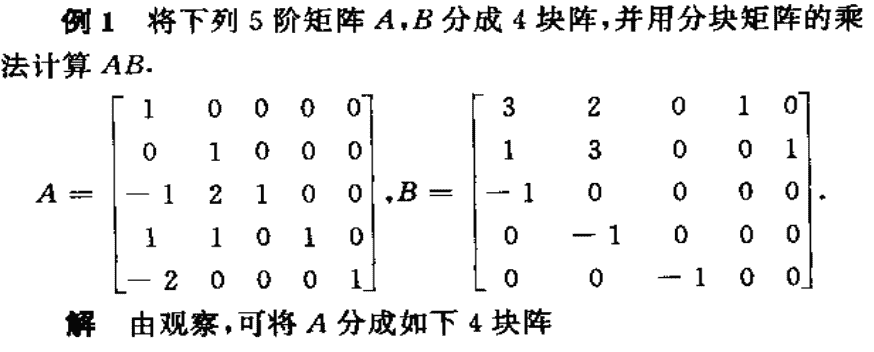
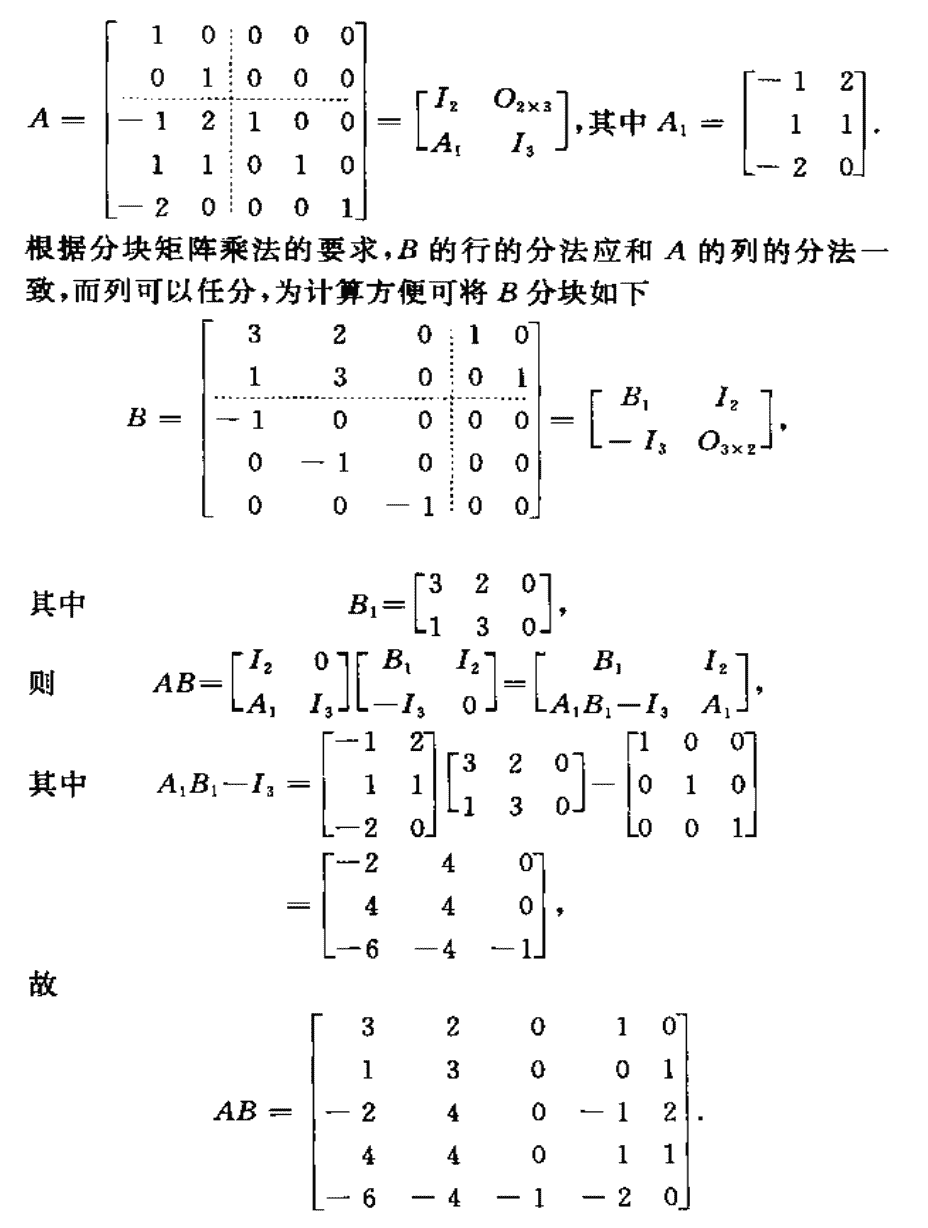
2. 分块矩阵乘法：对于的两个矩阵相乘，假设把矩阵横切刀，竖着切刀(你就想象一下家里切豆腐凉拌),矩阵横着切刀，竖着切刀，显然分块后也是对应每一行x每一列。最后乘起来得到的是块油炸豆腐 矩阵。但由于分块乘法，乘法本身也是矩阵乘法，所以也要满足块的列数=块的行数。所以在豆腐下锅矩阵分块乘法前，第一个矩阵竖着切的每一刀的宽度要和第二块豆腐横着切的每一刀宽度相同

   (脑子全是香喷喷的铁锅油炸豆腐，浇上味极鲜酱油撒上葱花后热气腾腾地出锅……)

E.g.

想看例子请戳我，不想看可忽略

截图自^[1]P82

3. 分块矩阵的转置(自己想，想不出来wiki去)
4. 分块矩阵的逆矩阵：

对角分块阵(假如都可逆)

普通矩阵，分成几块后做乘法，比如设:

可得

这样可以把一个高阶的矩阵求逆问题转化成低阶矩阵求逆问题。结合分治法和一些奇奇怪怪的trick，可以像矩阵乘法一样从进行时间复杂度优化。

5. 分块矩阵的初等变换(以为例， 以后填坑)

分块对换阵

分块倍乘阵

分块倍加阵

线性方程组

这一块讲的非常简略，因为学过线代的人大多数这一章掌握的比较牢靠(往往相似矩阵，矩阵分解，二次型那一块快到期末，掌握得通常不太好)。所以省下笔墨只零零星星地提几点。

1. （非常重要） 线性无关 仅有0解
2. （非常重要）极大线性无关组的定义。(此外，极大线性无关组可以作为方程组的一个基础解系)
3. （非常重要）齐次线性方程组基本定理：基础解系的向量数量= (从这里可以看出齐次方程组的解空间是的子空间， 正因为系数矩阵有了秩(序)，才导致解空间维度比原来的空间小了，变成了基础解系的向量数量)
4. 线性方程组基本定理：是否有解(判别条件)；通解和特解。
5. 具体计算：化简为Hermitte标准形(行阶梯矩阵标准型)。

“有的人天生就是战士。他/她不会惧怕一切困难，也不会为一切失败与挫折低头，因为他/她的目标是星辰大海”⭐️

参考文献

1. 《线性代数》 第二版 居余马 清华大学出版社 ↩︎
2. 《矩阵理论与应用》 张跃辉 上海交通大学出版社 ↩︎