课程笔记：强化学习(2)——Bellman方程的动态规划求解

动态规划

本节只是非常粗略的把动态规划的要点总结一下，是课堂笔记纲要，并非详细讲解。先占个坑，以后有空再补

1. 动态规划需要满足的条件：

   1. 最优子结构(Optimal substructure):

   • 原问题的最优解一定也是子问题的最优解。例如，一个输入长度为N的序列的某个Scheduling问题（记为T(1，N) ) 的最优解，拆分后一定也是其子问题T(1,N/2-1), T(N/2, N)的最优解。

   • 问题的最优解可以通过某种形式组合和计算，得到原问题的最优解

   2. 重叠子问题
   • 子问题与原问题有同样的format和structure
   3. 无后效性
   • 计算原问题最优解时，不会对子问题最优解产生影响。

马尔科夫链和马尔科夫决策过程满足上述三个条件的，因为:

• Bellman方程将原问题递归的分解为规模更小的子问题
• 子问题拥有同样的format和structure
• Que？ 有疑问，虽然马尔科夫过程强调每个state只与上一个state有关，与其他state无关(

2. Dynamic Planning in MDP:

   1. For prediction(Policy Evaluation):

   Input: MDP 和策略 or MRP (没有显示的策略表示，是Implicit Policy) Output: value function 对Policy Evaluation的理解：给定一个策略，通过贝尔曼方程迭代求出所有状态的价值

   ii.For control:

   Input: MDP

   Output: 最优价值函数 和最优策略

3. Bellman方程:

(State-) Value Function:

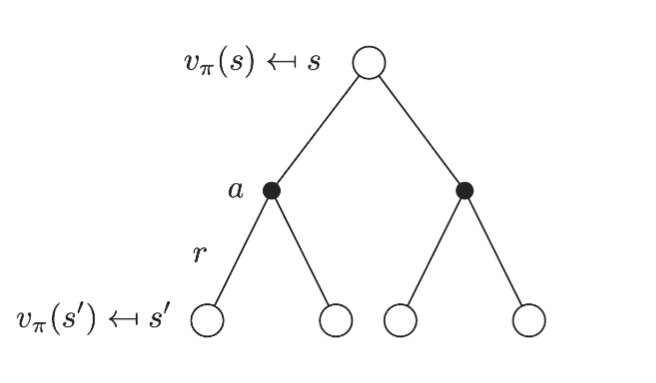
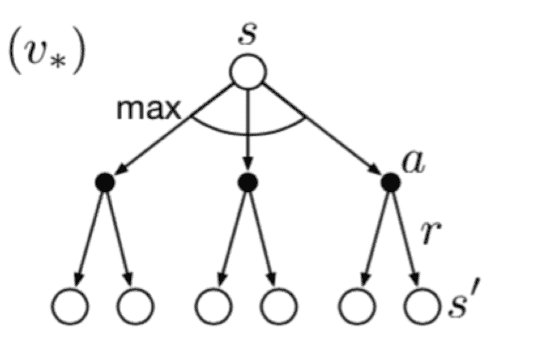
求Optimal (把求期望操作找操作)：

Action Function:

求Optimal 时(把求期望操作找操作)：

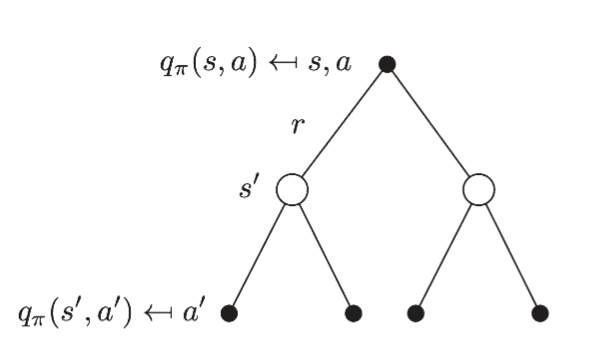
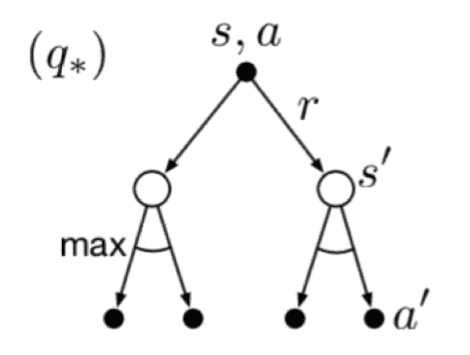
Policy Evaluation

image-20210929211939079

给定一个policy ，评估/衡量在 下每个状态的value function.

Policy Iteration

image-20210929212427612

这个是通过贪心的策略来迭代得到最好的policy。基本思想是，即在state function 固定情况下，通过贪心的选择给自己带来最大受益的action a 来作为自己的策略。可以证明经过多次迭代后，策略能收敛到贪心策略下的最优解上。

Value Iteration

image-20210929213203328

这个的特点是没有给定任何显示的(explicit)策略, 而是只求解state function。

与Policy Evaluation 和Policy Iteration 不同， 前两者都出现了这个东西，也就是说每个状态下选择某个动作的概率是被记录的，并且可能随着算法也会迭代更新；而Value Iteration 每次选择受益最大的动作来更新value。

等迭代结束，value全部求出来后，最后一遍求解。

Summary

image-20210929213757669