课程笔记：统计学习理论与方法（ELS_Chap7）

📚书籍：《Elements of Statistical Learning》Chap 7

两个概念

1. 模型选择(Model Selection): 模型由参数控制的，模型选择既包括模型类型选择，也包括参数的控制。后面讲贝叶斯信息准则时(BIC)会讲到。
2. 模型评估(Model Assessment): 给定一个模型，评估其训练误差(In-sample Error)，测试误差(Extra-sample Error)，泛化误差(Generalization Error)。评估训练误差与测试误差之间的差距Bound.

两者都是侧重对模型的泛化误差进行评估，而非模型的训练误差。泛化误差是整个统计学习中最核心的关注问题。

训练误差与泛化误差

训练误差： 泛化误差： 其中损失函数通常是:

• 均方误差
• 对数极大似然函数【用于多分类】(严格来说这不算损失函数，但是极大似然最大等价于加符号最小，所以可以写成相同形式): .其中相当于真实标签(Ground Truth).
• 对数极大似然的特殊情况【0-1分类】：

📢注意，我们算误差时的Ground Truth(GT) 并不一定是真实的标签，因为获取数据的过程中无法避免有噪声存在(就比如用精密物理仪器测量的结果总会有无法避免的系统误差)。我们的损失函数是让模型的估计值和GT算误差，不是和算误差。

Bias-variance 分解

假设： 是从某个数据分布中采样得到的某个数据集。数据的真实分布是，数据的真实标签是，但是我们获取数据集时总会有噪声干扰。通常假设噪声服从均值为0的某个高斯分布。

考察在一点上的单点泛化误差，其中求期望操作是对所有的数据集求的期望(Expectation over all the dataset ).也就是说在这里，也是随机变量，它的随机性来源于可能选取不同的数据集 ；而的随机性只来源于，二者独立无关联。

关于期望与方差的常用性质，请参见这篇👉博客。

KNN的例子

KNN的模型是. 为了计算方差方便， 在理论推导这里做了一个重要近似：因为KNN取的是K个近邻点来插值估计，所以假设认为他们的“本源”.这样，KNN的方差可以如下计算: 故泛化误差拆分为: 可以看出越小，模型复杂度越大，方差越大，bias应该会越小。

线性回归的例子

对于线性回归函数 , 解最小二乘误差下的最佳近似参数是

故.可以看出的随机性来源于y，即来源于 .（这与刚才说法不矛盾。因为之前对的分析是抽象的符号，而这里是对线性回归具体公式分析） 故

训练误差: 可以看出模型复杂度由数据量和参数量共同控制。

这部分的推导需要用到矩阵的迹的性质：

乐观度

乐观度(Optimisim)的概念主要是为了比较模型训练误差与泛化误差之间的差距，或者如何用训练误差去估计泛化误差。

直接计算训练误差和泛化误差的差有困难，因为模型输入都不固定。所以可以采用重采样的技术，原先训练集,是训练时采样得到的标签，记为；重采样是对相同的, 再次采样。

结论 证明过程后续再补。

若是由参数量为线性回归得到的估计，那么 可得到

有效参数量

有效参数数量(Effective Number of Parameters): 对于线性回归，有如下关系：

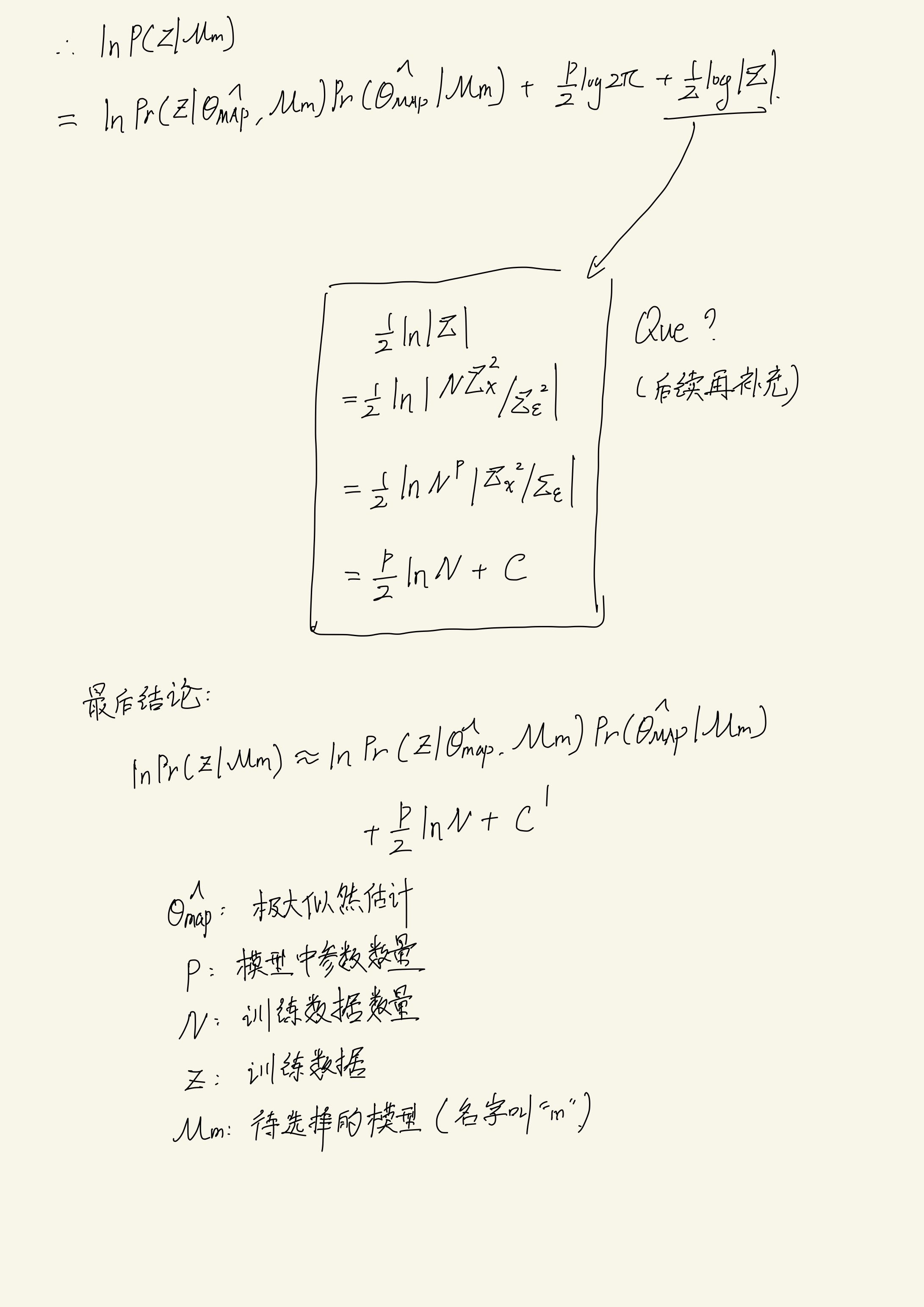
贝叶斯信息量（BIC）

题外话：前面的部分主要讲述的模型评价(Model Assesment)部分，贝叶斯信息量主要讲述的是模型选择的部分

BIC for 极大似然回归 BIC under Gaussian Model 他的Motivation是源自贝叶斯派的思想(下面手抄草稿，由于过程有点难，整理后还有很多错误比如符号上下标对不上)

1

2

3

交叉验证(以后有空再补)