课程笔记：统计学习理论与方法(ELS_Chap2)

📚书籍：《Elements of Statistical Learning》Chap 2

符号约定

输入变量(Input Variable)	, 通常随机变量取值是维随机向量(),其每个分量可用下角标表示是该维度特征的变量
(随机)变量的第i个观测值	, 可以是向量或标量
模型输出	Quantative Outputs:, Category: ； 模型预测值
矩阵	大写加粗正体，如个维度为的向量组成的矩阵
向量	约定:普通的维向量表示成，不用加粗; 而维度为N时，若加粗为，代表的是随机变量第个特征分量的所有观测值(N个观测值)组成的向量。E.g. 是矩阵的第行，是矩阵的第列。所有的向量规定为列向量的形式。

统计学习的重要原则

Statistical Learning的目标是为了最好的泛化性能(Best Generalization Property)而不是最小的训练误差(Minimum Training Error)

线性回归

1. 设输入是一个列向量, 其每个维度分量下标是 写成矩阵形式，其中

2. 线性回归的误差函数衡量方式——最小二乘

3. 从最小化误差函数的方式，对求导，得：

4. 思考一下两种数据分布情况对线性回归模型影响：

   1. 训练数据中的每一类都是服从高斯分布，而且每一类的方差一样但是均值不同。
   2. 某一类的训练数据是由多个高斯分布合成的，可能高斯分布的方差和均值都不太一样，

   对于第1种情况线性回归是比较optimal的，但是对于第二种效果比较差。

   而K近邻算法对于第2中情况相对会更suitable.

   (先占坑，后续补上解释)

   如下图所示，先从和 中分别随机采样10个sample(共计20个)，前十个作为类别1的均值，后十个作为类别2的均值。然后每个类中各生成100个sample，每个sample都是从采样，而每次是从该类中的10个中等概率()抽样得到。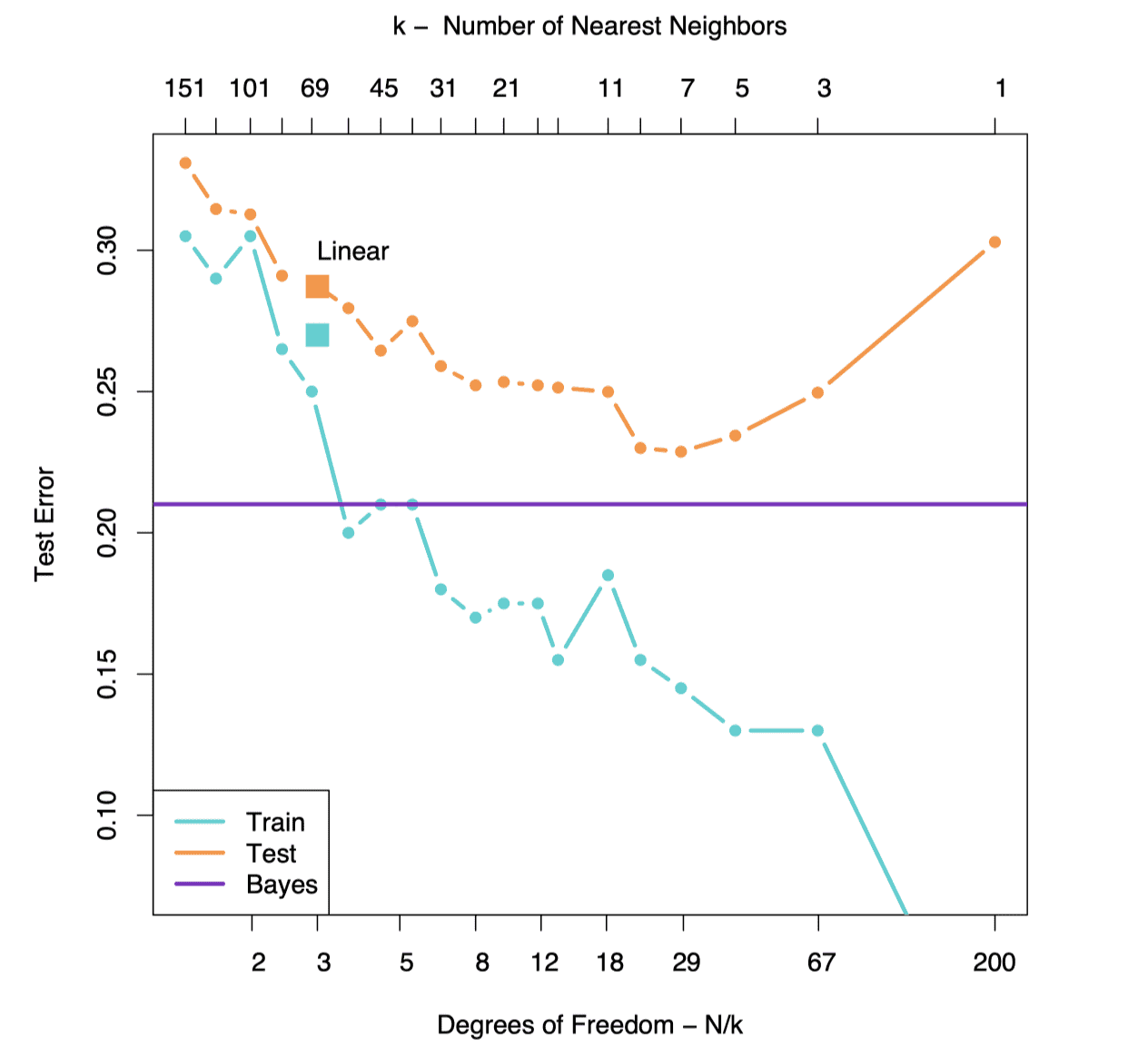

   

   圆点连线代表的K近邻的Error曲线，两个方块代表三元线性回归的Error值。可以看到:

   • 随着值变小，K近邻模型自由度在变大，模型复杂度在上升。模型逐渐由欠拟合转变为过拟合。后面也会讲解
   • 可以看到在这种多高斯分布混合采样得到的数据集中，K近邻最好的Error要比线性回归好。

K近邻

1. 几何意义：

   在特征空间中，对每个训练实例点,距离该点比其他点更近的所有点组成一个区域，叫做单元(Cell).每个训练实例点都拥有一个单元，所有训练实例点的单元对特征空间构成一个划分。 ^[1]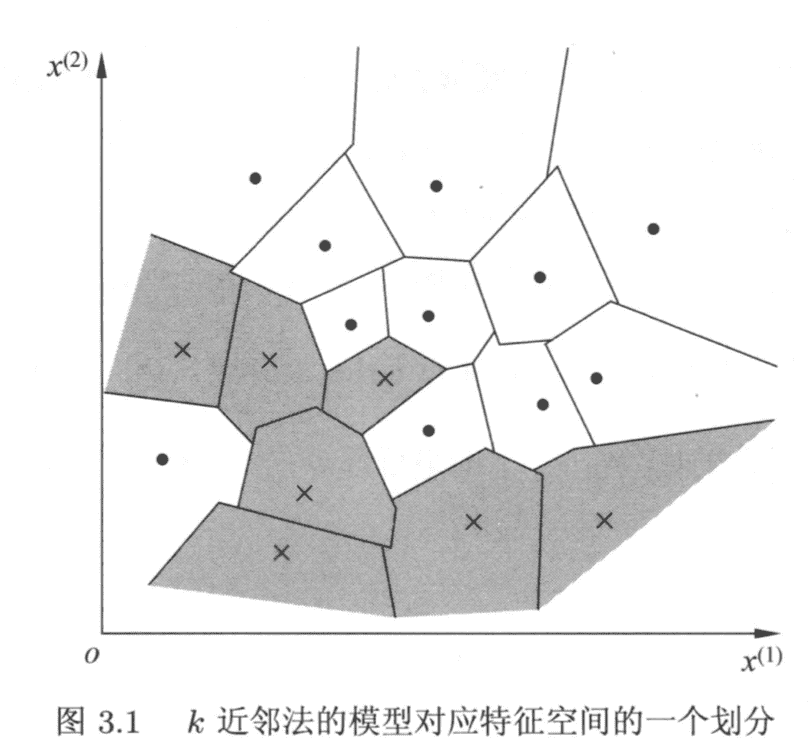

2. 具体内容参见李航《统计学习方法》Chap3 课程笔记(先占坑，后面补上笔记后建立链接🔗)

统计决策理论(Statistical Decision Theory)

根据模型选择(Model Selection)的理论，通过最小化期望预测误差(Expected Prediction Error, EPE)来确定模型中的参数选择，从而确定模型。

对于回归问题的EPE

对于回归问题(不仅仅是线性回归)，大多采用最小均方误差的方法计算误差: 故，若想使得EPE取最小值，只需让对于每个, 使得最小即可(逐点最小化)，可得 故

含义解释： 理论上期望预测误差最小的回归函数模型，在最小二乘误差意义下，每个训练数据当时，取的平均值()是能够达到的。

注意，在这里我们认为所有训练数据的与是两个独立的随机变量，分别取样自不同的分布中组成了联合概率分布。这是一个重要的assumption，也是统计学习里的基本思路。

另外可以拓展为,在某个邻域附近的所有样本的值取平均。

关于期望 和 ，条件期望中的角标，随机变量和事件区别，符号大小写的不同意义等细微区别，参见随笔XXX（先占坑），以帮助理解。--- 2021.10.08 简要补充 首先要区分随机变量和事件，比如对于随机变量, 是一个事件，即取一个固定的值这件事情发生了，所以是一个事件。而随机变量自身是有可能取任何一个值的，只不过有不同的概率(所以为什么随机变量会有概率分布这个概念)。 所以我们说条件期望时，就是指，即在事件发生的条件下，取各种值的可能性的期望。 。 此外事件的独立和变量的独立不是一回事。n个事件的独立要求n个事件两两独立，任意三个独立，任意四个独立……任意n个独立。但是随机变量的独立只需要 一个条件即可。因为每个随机变量可以取很多值，包含了很多的事件，所以显然约束要比事件独立 要强得多。 在信息论中，信息熵和条件熵，互信息与条件互信息中，条件部分是随机变量还是事件是大有讲究的。比如见此图： 以互信息和的关系为例，如下图公式所示 对于条件信息熵:

对于分类问题的EPE

先做一些符号约定：

分类问题的输出是离散型(随机)变量，定义其符号为 (Group),属于同一类的值在同一个Group里，以此来表示类别信息。 同理，通过逐点最小化，只需要 原因比较显然，哪个样本属于类的概率大，并且损失函数对于分类错误的惩罚大小共同决定了EPE。对于二分类+ 0-1 Loss来说(分类正确L为0，否则L为1)，那么可得 这个分类方式被称为贝叶斯分类器（Bayes classification）: 我们通过把样本分类到最可能的类别中(classify to the most probable class)。贝叶斯分配器得到的Error Rate(Bayes Rate)是所有分类模型中统计学理论上误差最小的。

经过刚才的讲解，读者应该能较为清楚的感受到，统计学习中把,作为两个独立的随机变量研究他们的联合分布，本质上研究的是数据与Label的相关性信息。即几乎目前绝大多数有监督学习的方法(机器学习,深度神经网络等)本质上都是学习数据与Label的分布和相关性信息。所以说这类模型是数据驱动(data-driven)的，机器并没有理解数据，只是学习到数据的分布而已。

k近邻及其Majority Vote选出类别的机制，本质上也是通过训练数据去近似。而当时，K近邻近似得到。通过这个例子，我们也发现EPE的结果在回归和分类问题上本质上是一致的。

Bias-Variance Decomposition

先考虑在某个点上的MSE拆分：

设训练集为, 函数为准确的预测模型(has no bias), 计算这一测试点(test point)上的最小均方误差。由于为精准模型，因此其变化只与输入有关，因此在的期望上可以看做是常数，就有如上变换。

其中第一项是预测模型自身的方差， 第二项是预测模型与真实模型之间的Bias。对于方差来说，是由于对计算时带来的数据方差(通常假设是的高斯噪声，方差由此带来)。对于Bias而言，一方面由于在的邻域里采样，另一方面由于预测模型总会有误差(高斯噪声的均值)。

注意这里算MSE拆分时的与数据集中的随机变量的取值不等价的。因为数据集中的标签往往充满噪声的，而我们假设理想数据集是满足某种分布，然后再该分布上加上噪声才得到了数据集中的真实的。所以算bias时 是不能写成的。 后面我们算EPE的拆分时，把数据集中的真实放了进去，因此拆分中多了关于噪声的方差项。详细见下面介绍。

对于线性回归模型

假设数据集 中与 成近似线性分布，假设中间差个高斯噪声

由于

可得到 故知道对于的估计是无偏估计，因而得到在均方误差中线性回归模型满足即, bias 为0。

并且在这一测试点(test point) 下面，我们对整个数据集(over training set )的EPE进行bias-variance拆分。先考虑固定, 让变

维度灾难(Curse of Dimensionality)

待填坑

模型选择与误差(Model Selection and Bias)

参考文献

1. 《统计学习方法》第二版 李航 ↩︎